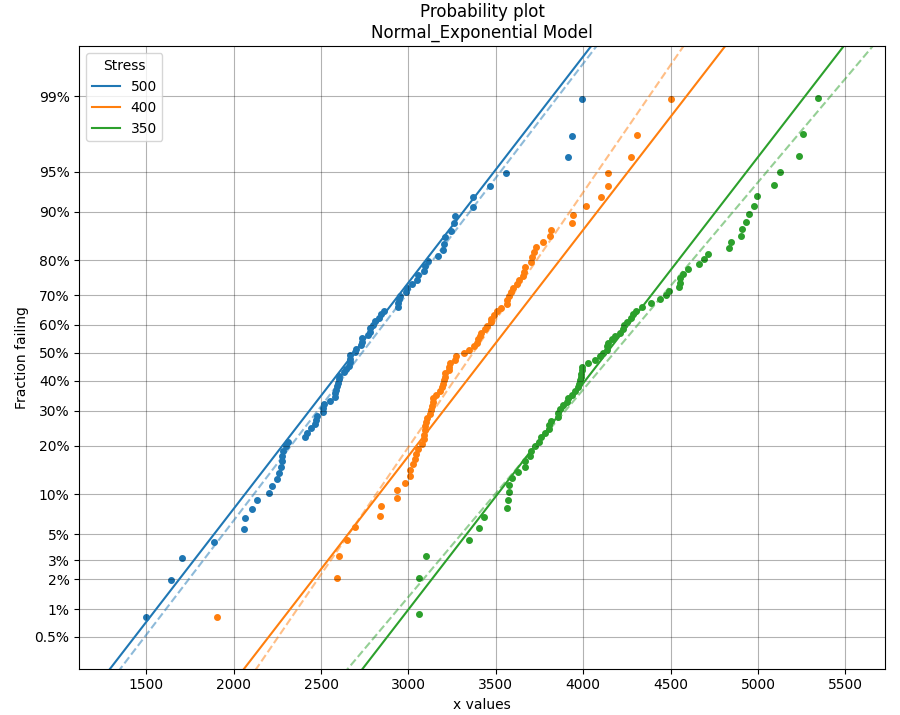
What does an ALT probability plot show me
An ALT probability plot shows us how well our dataset can be modeled by the chosen distribution. This is more than just a goodness of fit at each stress level, because the distribution needs to be a good fit at all stress levels and be able to fit well with a common shape parameter. If you find the shape parameter changes significantly as the stress increases then it is likely that your accelerated life test is experiencing a different failure mode at higher stresses. When examining an ALT probability plot, the main things we are looking for are:
Does the model appear to fit the data well at all stress levels (ie. the dashed lines pass reasonably well through all the data points)
Examine the AICc and BIC values when comparing multiple models. A lower value suggests a better fit.
Is the amount of change to the shape parameter within the acceptable limits (generally less than 50% for each distribution).
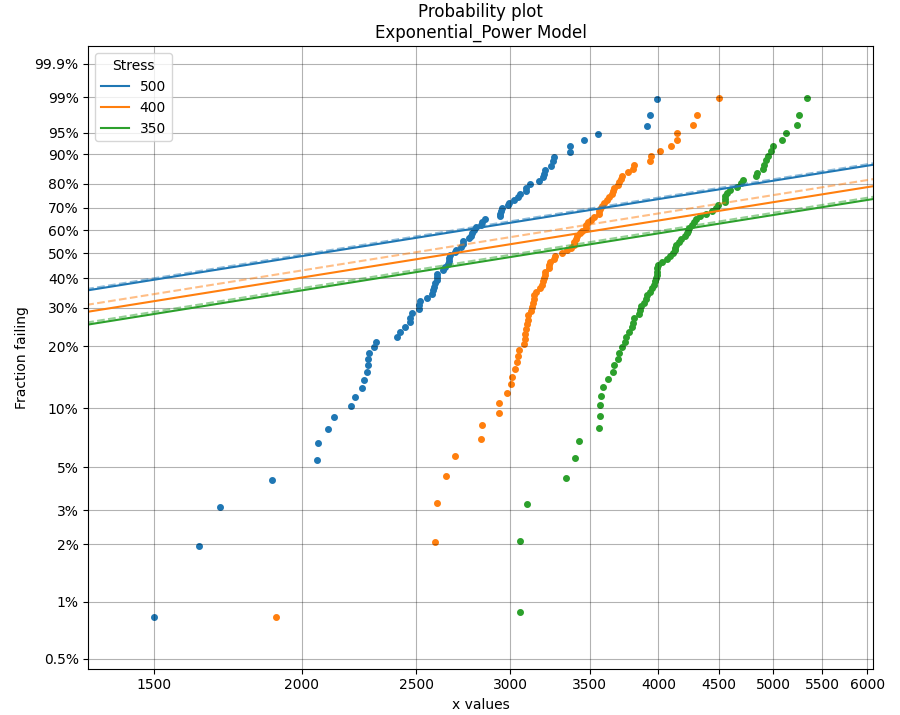
The following example fits 2 models to ALT data that is generated from a Normal_Exponential model. The first plot is an example of a good fit. The second plot is an example of a very bad fit. Notice how a warning is printed in the output telling the user that the shape parameter is changing too much, indicating the model may be a poor fit for the data. Also note that the total AIC and total BIC for the Exponential_Power model is higher (worse) than for the Normal_Exponential model.
If you are uncertain about which model you should fit, try fitting everything and select the best fitting model.
If you find that none of the models work without large changes to the shape parameter at the higher stresses, then you can conclude that there must be a change in the failure mode for higher stresses and you may need to look at changing the design of your accelerated test to keep the failure mode consistent across tests.
Example 1
from reliability.Other_functions import make_ALT_data
from reliability.ALT_fitters import Fit_Normal_Exponential, Fit_Exponential_Power
import matplotlib.pyplot as plt
ALT_data = make_ALT_data(distribution='Normal',life_stress_model='Exponential',a=500,b=1000,sigma=500,stress_1=[500,400,350],number_of_samples=100,fraction_censored=0.2,seed=1)
Fit_Normal_Exponential(failures=ALT_data.failures, failure_stress=ALT_data.failure_stresses, right_censored=ALT_data.right_censored, right_censored_stress=ALT_data.right_censored_stresses,show_life_stress_plot=False)
print('---------------------------------------------------')
Fit_Exponential_Power(failures=ALT_data.failures, failure_stress=ALT_data.failure_stresses, right_censored=ALT_data.right_censored, right_censored_stress=ALT_data.right_censored_stresses,show_life_stress_plot=False)
plt.show()
'''
Results from Fit_Normal_Exponential (95% CI):
Analysis method: Maximum Likelihood Estimation (MLE)
Failures / Right censored: 240/60 (20% right censored)
Parameter Point Estimate Standard Error Lower CI Upper CI
a 501.729 27.5897 447.654 555.804
b 985.894 70.4156 857.107 1134.03
sigma 487.321 22.1255 445.829 532.674
stress original mu original sigma new mu common sigma sigma change
500 2733.7 482.409 2689.22 487.321 +1.02%
400 3369.57 432.749 3456.02 487.321 +12.61%
350 4176.89 531.769 4134.25 487.321 -8.36%
Goodness of fit Value
Log-likelihood -1833.41
AICc 3672.89
BIC 3683.93
If this model is being used for the Arrhenius Model, a = Ea/K_B ==> Ea = 0.04324 eV
---------------------------------------------------
Results from Fit_Exponential_Power (95% CI):
Analysis method: Maximum Likelihood Estimation (MLE)
Failures / Right censored: 240/60 (20% right censored)
Parameter Point Estimate Standard Error Lower CI Upper CI
a 4.23394e+06 1.10593e+07 25314.2 7.0815e+08
n -1.16747 0.433666 -2.01744 -0.317497
stress weibull alpha weibull beta new 1/Lambda common shape shape change
500 2937.9 5.99874 2990.79 1 -83.33%
400 3561 8.20311 3880.84 1 -87.81%
350 4415.41 8.3864 4535.54 1 -88.08%
The shape parameter has been found to change significantly (>50%) when fitting the ALT model.
This may indicate that a different failure mode is acting at different stress levels or that the Exponential distribution may not be appropriate.
Goodness of fit Value
Log-likelihood -2214.94
AICc 4433.93
BIC 4441.3
'''
References:
Probabilistic Physics of Failure Approach to Reliability (2017), by M. Modarres, M. Amiri, and C. Jackson. pp. 136-168
Accelerated Life Testing Data Analysis Reference - ReliaWiki, Reliawiki.com, 2019. [Online].