Optimal replacement time
When conducting maintenance planning, we must optimise the frequency of preventative maintenance (PM) for the minimum overall cost. If PM is conducted too frequently then we will have high costs, but if not conducted often enough then failures will result and we incur the higher cost of corrective maintenance (CM). Depending on the underlying failure distribution, it is possible to model these costs for a range of PM intervals, with the lowest cost per unit time resulting from the optimal replacement time. This function calculates the cost per unit time to determine how cost varies with replacement time. The cost model can be used for HPP (ie. the maintenance makes the system “as good as new”) or Power Law NHPP (ie. the maintenance makes the system “as good as old”). The default is for “as good as new”.
Cost in the above context should include all associated costs of PM and CM. These are not just the costs associated with parts and labor but may also include other costs such as system downtime (which may vary between PM and CM), loss of production output, customer satisfaction, etc. Some of these costs are difficult to quantify but organisations should strive to quantify all the costs of PM and system failure (requiring CM) if they want to accurately optimise their maintenance schedule.
API Reference
For inputs and outputs see the API reference.
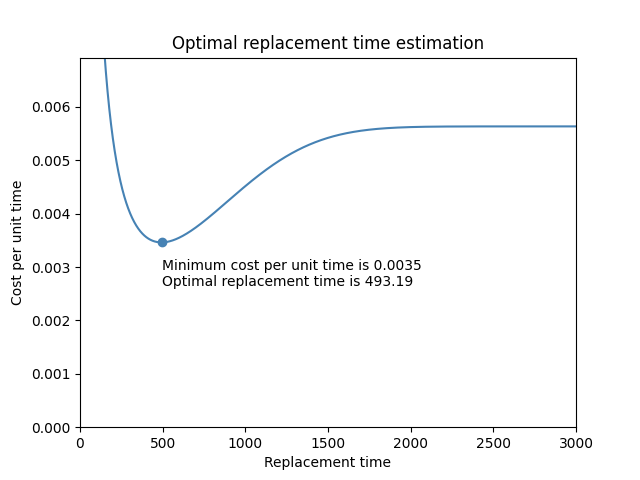
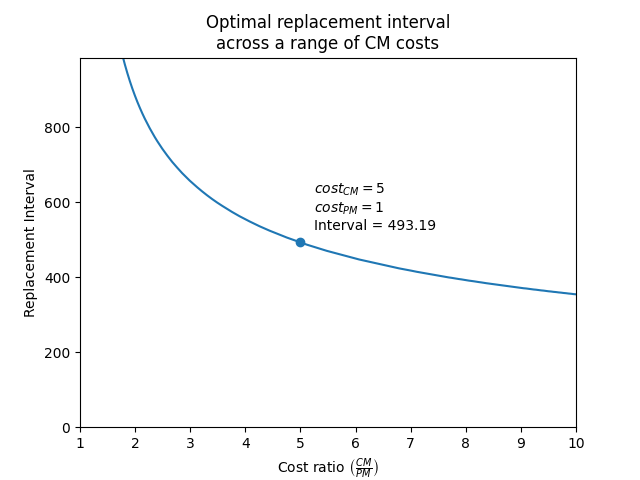
In the example below, we provide the cost of preventative maintenance (cost_PM), and the cost of corrective maintenance (cost_CM), as well as the Weibull parameters of the failure distribution. Leaving the default outputs, we obtain a plot of the cost per unit time and the printed results. This example is based of the example provided on the reliasoft article.
from reliability.Repairable_systems import optimal_replacement_time
import matplotlib.pyplot as plt
optimal_replacement_time(cost_PM=1, cost_CM=5, weibull_alpha=1000, weibull_beta=2.5,q=0)
plt.show()
'''
Results from optimal_replacement_time:
Cost model assuming as good as new replacement (q=0):
The minimum cost per unit time is 0.0035
The optimal replacement time is 493.19
'''