---

Kolmogorov-Smirnov test

The Kolmogorov-Smirnov test is a statistical test for goodness of fit to determine whether we can accept or reject the hypothesis that the data is from the specified distribution at the specified level of significance. This method is not a means of comparing distributions (which can be done with AICc, BIC, and AD), but instead allows us to accept or reject a hypothesis that data come from a distribution. Unlike the chi-squared test, the Kolmogorov-Smirnov test does not depend on the bins of a histogram, therefore making it a more consistent goodness of fit.

The procedure for the test involves comparing the fitted CDF (from a hypothesised distribution) against the empirical CDF (calculated using a rank order of the data of the form i/n). The difference between the fitted CDF and the empirical CDF is used to find the Kolmogorov-Smirnov statistic. The specified level of significance (analogous to confidence level) and the number of data points is used to obtain the Kolmogorov-Smirnov critical value from the Kolmogorov-Smirnov distribution. By comparing the Kolmogorov-Smirnov statistic with the Kolmogorov-Smirnov critical value, we can determine whether the hypothesis (that the data are from the specified distribution) should be rejected or accepted. The acceptance criteria is when the the Kolmogorov-Smirnov statistic is below the critical value.

API Reference

For inputs and outputs see the API reference.

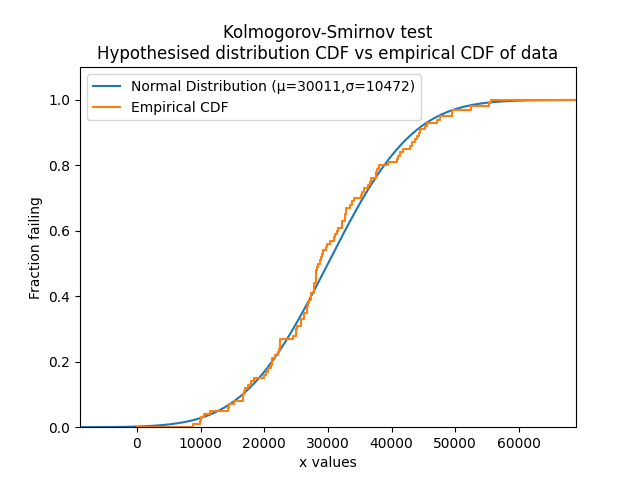
In the example below we import a dataset called mileage which contains 100 values that appear to be normally distributed. Using the function KStest we can determine whether we should accept the hypothesis that the data are from a Normal distribution with parameters mu=30011 and sigma=10472.

from reliability.Datasets import mileage
from reliability.Distributions import Normal_Distribution
from reliability.Reliability_testing import KStest
import matplotlib.pyplot as plt

data = mileage().failures
dist = Normal_Distribution(mu=30011, sigma=10472)
KStest(distribution=dist, data=data)
plt.show()

'''
Results from Kolmogorov-Smirnov test:
Kolmogorov-Smirnov statistic: 0.07162465859560846
Kolmogorov-Smirnov critical value: 0.13402791648569978
At the 0.05 significance level, we can ACCEPT the hypothesis that the data comes from a Normal Distribution (μ=30011,σ=10472)
'''