---

Stress-Strength interference

Stress-Strength interference is a model to predict the probability of failure when the stress and strength probability distributions are known. Failure is defined as when stress > strength. If both the stress and strength distributions are Normal Distributions, then there exists a simple analytical solution which will give an exact result. To calculate stress-strength intereference between distributions other than Normal Distributons requires the evaluation of an integral. These two cases are shown below using the functions stress_strength_normal (for two Normal Distributions) and stress_strength (for any two distributions).

Stress-Strength Interference for two Normal Distributions

The probability of failure for two Normal distributions is found using the equation:

\(\text{Probability of failure} =\Phi \left(\frac{\mu_{strength}-\mu_{stress}}{\sqrt{\sigma_{strength}^{2}+\sigma_{stress}^{2}}}\right)\)

Where \(\Phi\) is the standard Normal CDF with \(\mu=0\) and \(\sigma=1\)

API Reference

For inputs and outputs see the API reference.

Example 1

In this example, we will create a stress and strength distribution (both of which are Normal distributions), and leaving everything else as default, we will see the results plotted and printed.

from reliability import Distributions
from reliability.Other_functions import stress_strength_normal
import matplotlib.pyplot as plt

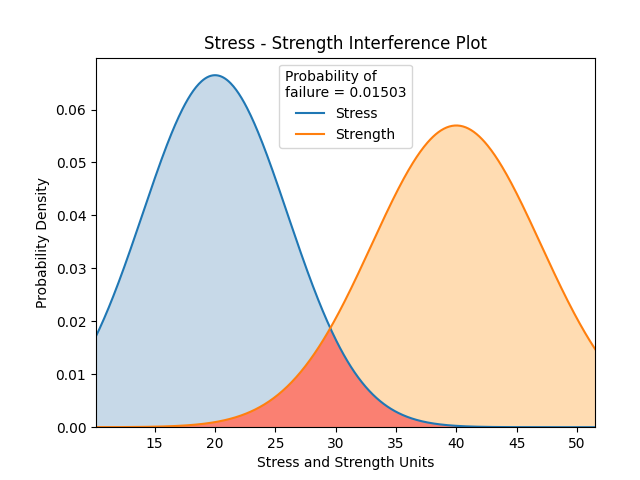
stress = Distributions.Normal_Distribution(mu=20,sigma=6)
strength = Distributions.Normal_Distribution(mu=40,sigma=7)
stress_strength_normal(stress=stress, strength=strength)
plt.show()

'''
Stress - Strength Interference
Stress Distribution: Normal Distribution (μ=20,σ=6)
Strength Distribution: Normal Distribution (μ=40,σ=7)
Probability of failure (stress > strength): 1.50298 %
'''

Stress-Strength Interference for any two Distributions

If either the stress or strength distributions are not Normal Distributions, the analytical method above can not be used and integration is required.

The equation to find the probability of failure any two distributions is:

\(\text{Probability of failure} =\int^{\infty}_{0} \left( f_{strength} \times R_{stress} \right)\)

Where \(f\) is the PDF and \(R\) is the SF. The above integral can be evaluated using the trapz function in numpy: probability of failure = np.trapz(strength.PDF(x) * stress.SF(x), x)

API Reference

For inputs and outputs see the API reference.

Example 2

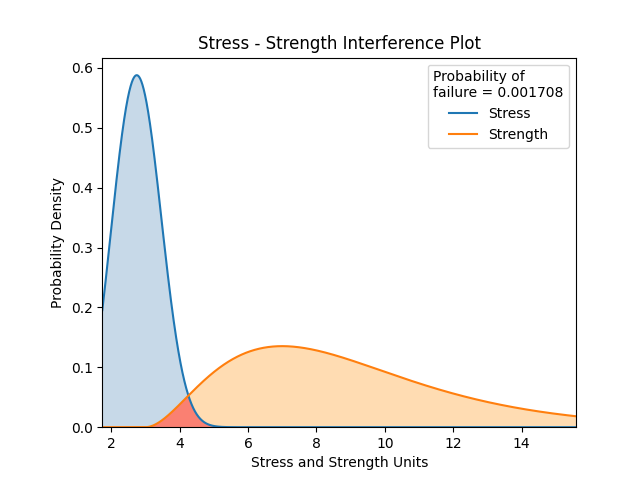
In this example, we will create a Weibull stress distribution and a Gamma strength distribution, and leaving everything else as default, we will see the results printed and the distribution plot.

from reliability import Distributions
from reliability.Other_functions import stress_strength
import matplotlib.pyplot as plt

stress = Distributions.Weibull_Distribution(alpha=2, beta=3, gamma=1)
strength = Distributions.Gamma_Distribution(alpha=2, beta=3, gamma=3)
stress_strength(stress=stress, strength=strength)
plt.show()

'''
Stress - Strength Interference
Stress Distribution: Weibull Distribution (α=2,β=3,γ=1.0)
Strength Distribution: Gamma Distribution (α=2,β=3,γ=3)
Probability of failure (stress > strength): 0.17078 %
'''